Trees

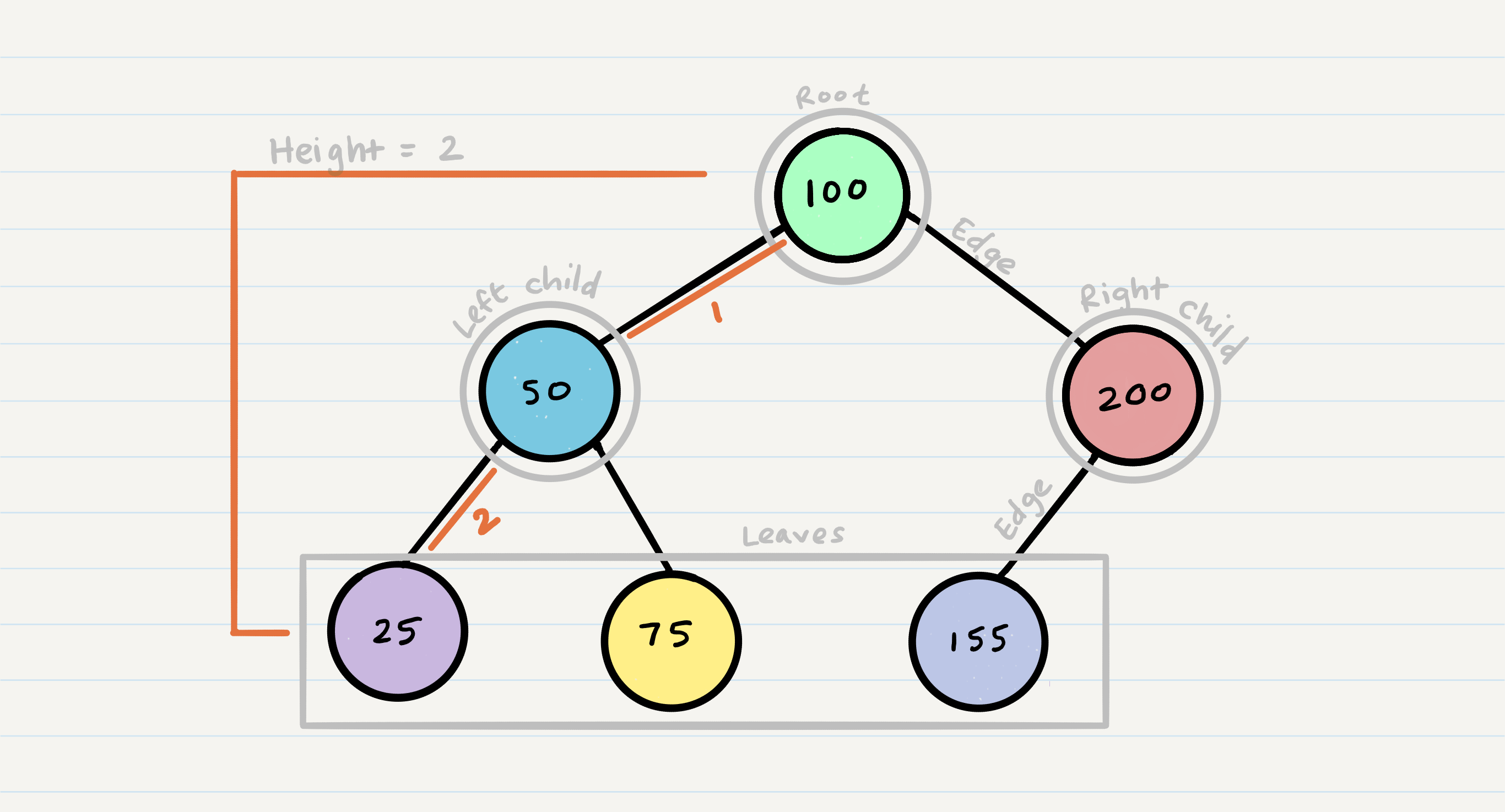
Trees Components

1. Node - A Tree node is a component which may contain its own values, and references to other nodes
2. Root - The root is the node at the beginning of the tree
3. K - A number that specifies the maximum number of children any node may have in a k-ary tree. In a binary tree, k = 2.
4. Left - A reference to one child node, in a binary tree
5. Right - A reference to the other child node, in a binary tree
6. Edge - The edge in a tree is the link between a parent and child node
7. Leaf - A leaf is a node that does not have any children
8. Height - The height of a tree is the number of edges from the root to the furthest leaf

Traversals

Traversing a tree allows us to:

• search for a node.
• print out the contents of a tree.

Types of traversing trees:

• Depth First
• Breadth First

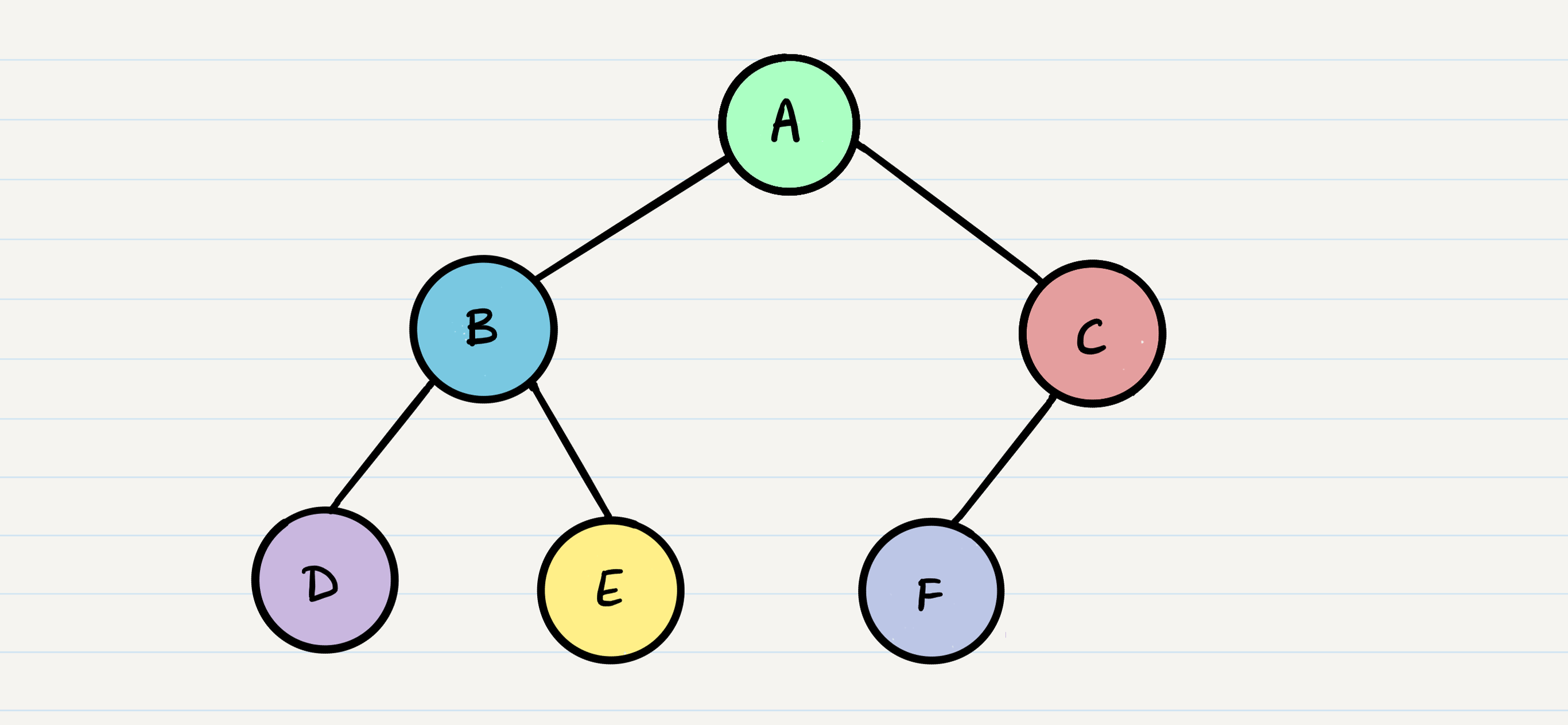
Depth first

it has different paths:

• Pre-order: root » left » right
• In-order: left » root » right
• Post-order: left » right » root

The most common way to traverse through a tree is to use recursion.

pseudocode for Depth first traversals

Pre-order

ALGORITHM preOrder(root)
// INPUT <-- root node
// OUTPUT <-- pre-order output of tree node's values

    OUTPUT <-- root.value

    if root.left is not Null
        preOrder(root.left)

    if root.right is not NULL
        preOrder(root.right)

In-order

ALGORITHM inOrder(root)
// INPUT <-- root node
// OUTPUT <-- in-order output of tree node's values

    if root.left is not NULL
        inOrder(root.left)

    OUTPUT <-- root.value

    if root.right is not NULL
        inOrder(root.right)

Post-order

ALGORITHM postOrder(root)
// INPUT <-- root node
// OUTPUT <-- post-order output of tree node's values

    if root.left is not NULL
        postOrder(root.left)

    if root.right is not NULL
        postOrder(root.right)

    OUTPUT <-- root.value

The biggest difference between each of the traversals is when you are looking at the root node.

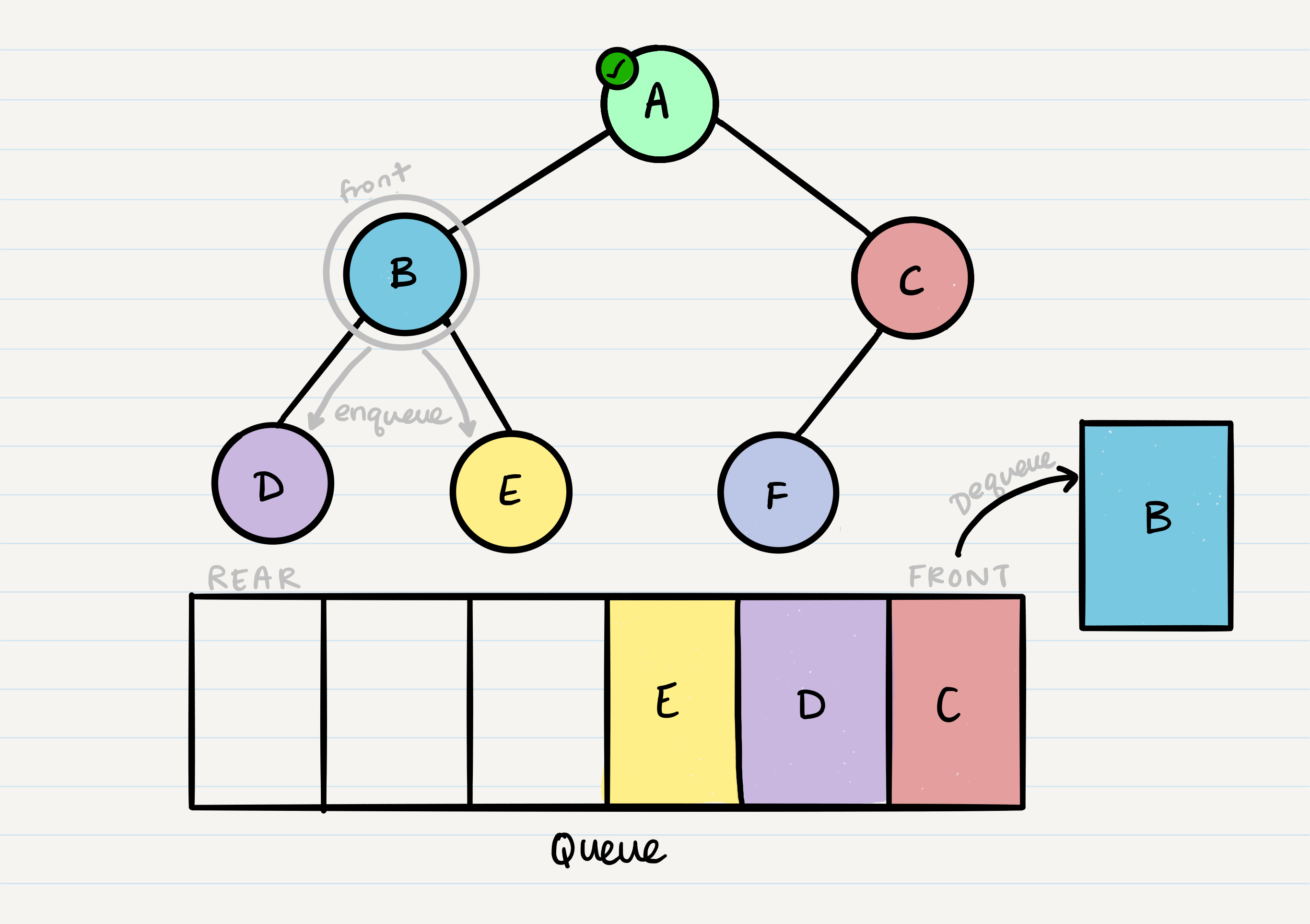
Breadth First

Iterates through the tree by going through each level of the tree node-by-node

• here the output is: A, B, C, D, E, F

breadth first traversal uses a queue instead of the call stack via recursion.

Pseudocode for Breadth First traversal

ALGORITHM breadthFirst(root)
// INPUT  <-- root node
// OUTPUT <-- front node of queue to console

  Queue breadth <-- new Queue()
  breadth.enqueue(root)

  while ! breadth.is_empty()
    node front = breadth.dequeue()
    OUTPUT <-- front.value

    if front.left is not NULL
      breadth.enqueue(front.left)

    if front.right is not NULL
      breadth.enqueue(front.right)

Binary Tree Vs K-ary Trees

Trees can have any number of children per node, but Binary Trees restrict the number of children to two.

• In K-ary trees we use K to refer to the maximum number of children that each Node is able to have.

Breadth First Traversal of k-ary

Pushing nodes into a queue, but moving down a list of children of length k, instead of checking for the presence of a left and a right child.

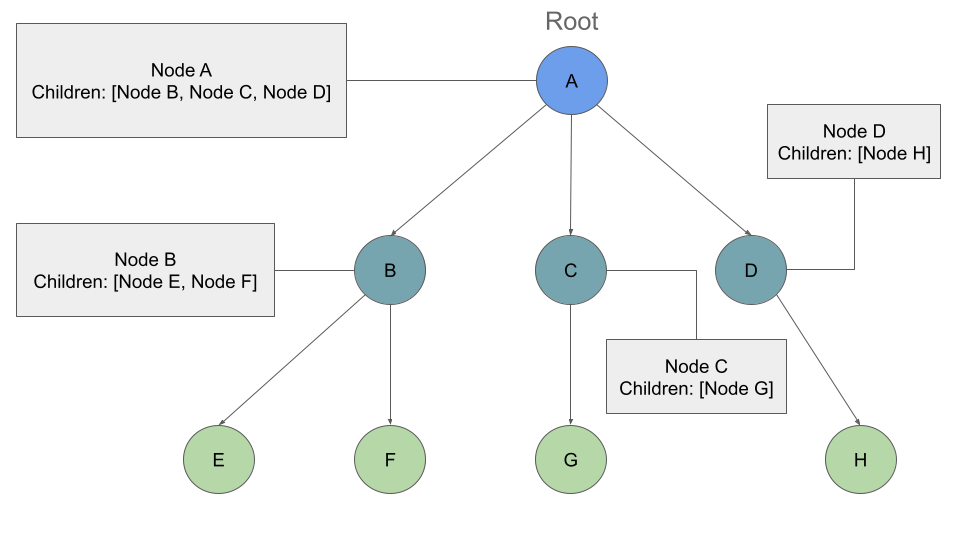
Output: A, B, C, D, E, F, G, H

Pseudocode of Breadth First of k-ary

ALGORITHM breadthFirst(root)
// INPUT  <-- root node
// OUTPUT <-- front node of queue to console

  Queue breadth <-- new Queue()
  breadth.enqueue(root)

  while ! breadth.is_empty()
    node front = breadth.dequeue()
    OUTPUT <-- front.value

    for child in front.children
        breadth.enqueue(child)

Adding a node

It doesn’t matter where nodes are placed in a binary tree. you might add it to the spot where one of the roots doesn’t have a left or a right, or for adding it to a specific location you need to reference both the new node to create, and the parent node which the child is attached to.

Big O

Time

• The Big O time complexity for inserting a new node is O(n)
• The Big O time complexity for searching a new node is O(n)

Space

• The Big O space complexity for a node insertion using breadth first insertion will be O(w) –> w is the largest width of the tree.

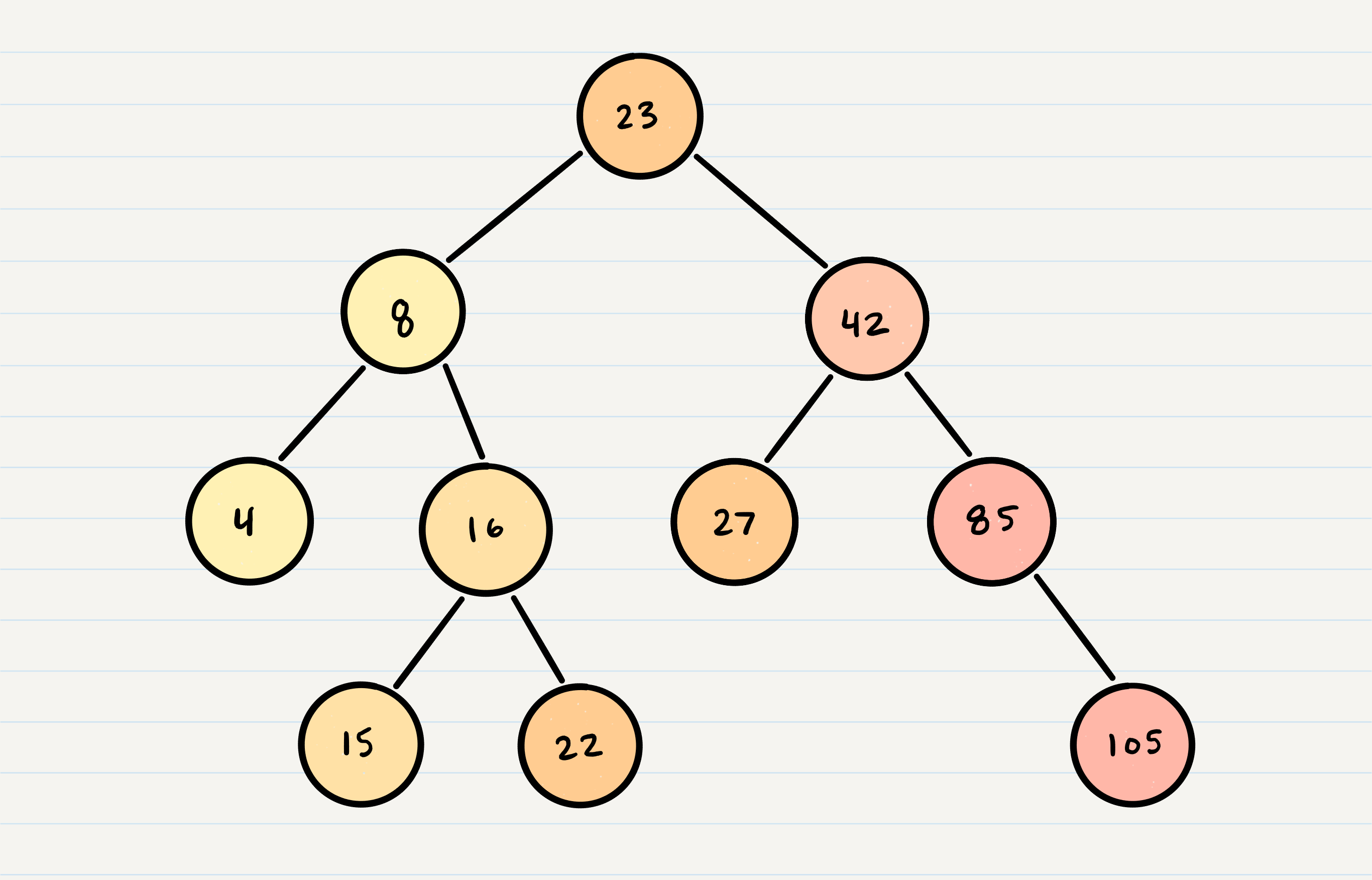
Binary Search Trees

A Binary Search Tree (BST) is a type of tree that does have some structure attached to it.

• All node values that are smaller than the root are placed to the left.
• All values that are larger than the root are placed to the right.

Searching a BST

Compare the node you are searching for against the root of the tree or sub-tree. If the value is smaller, you only traverse the left side. If the value is larger, you only traverse the right side.

The best way to approach a BST search is with a while loop. We cycle through the while loop until we hit a leaf, or until we reach a match with what we’re searching for.

Big O

Time

• The Big O time complexity of a Binary Search Tree’s insertion is O(h) –> h is height

• The Big O time complexity of a Binary Search Tree’s search is O(h)

• In a balanced (or “perfect”) tree, the height of the tree is log(n)
• In an unbalanced tree, the worst case height of the tree is n

Space

• The Big O space complexity of a BST search would be O(1)

More